1. Quick Sort

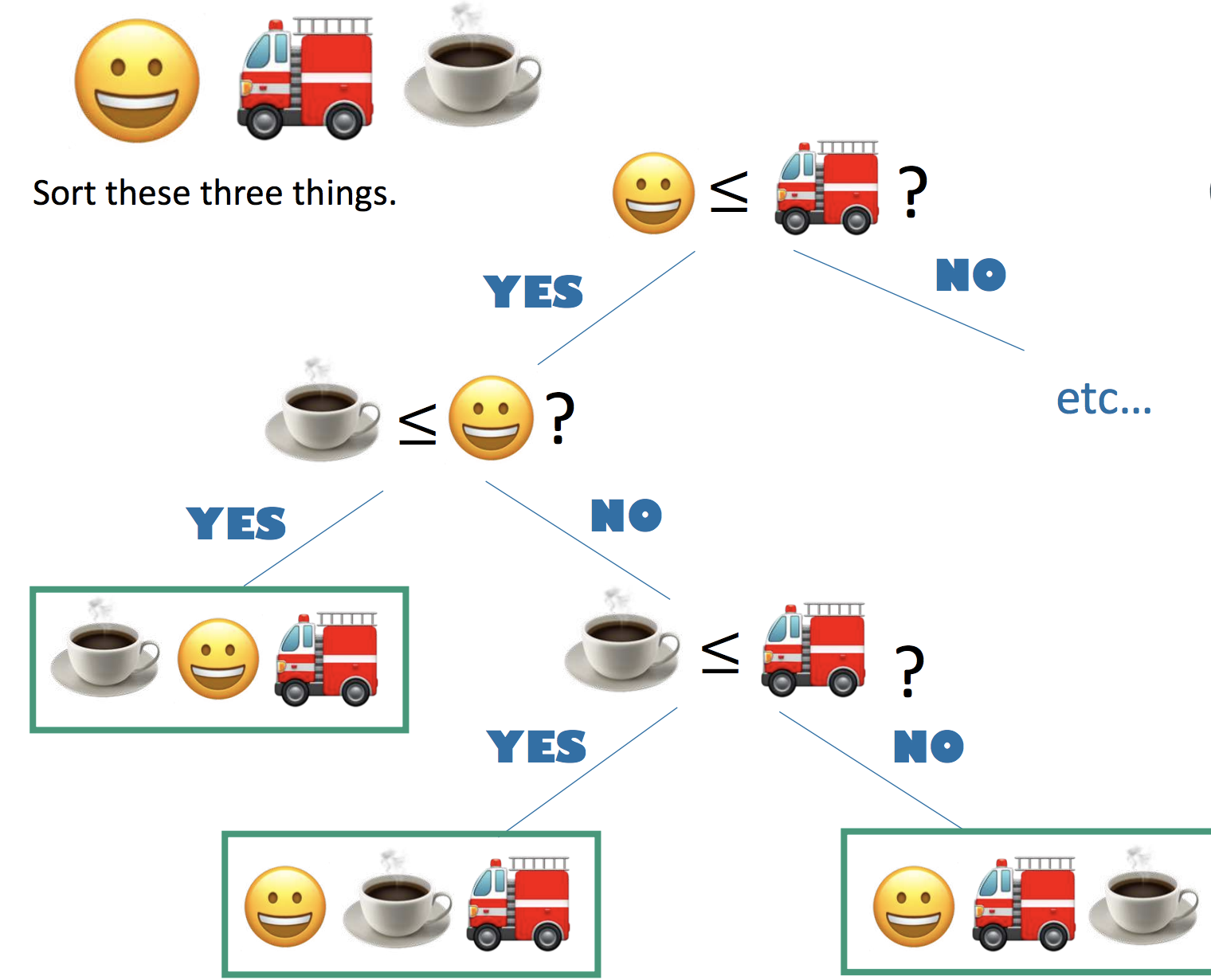
Giống như Merge Sort, Quick Sort cũng sử dụng chiến lược divide and conquer nhưng sử dụng thêm cả randomization để improve performance. Ý tưởng của Quick Sort như sau:

1. Pick 1 phần tử x làm pivot
2. Rearrange lại array A ban đầu thành [L,  x, R] trong đó: L gồm các phần tử < x và R gồm các phần tử > x
3. Tiếp tục làm như vậy (Recurse) trên L và R

Pseudo Code:

Pseudo Code ở trên rất dễ hiểu tuy nhiên chưa được tối ưu lắm do phải tách riêng L và R nên người ta (trong sách CLRS) implement theo 1 cách khác (in-place) hiệu quả hơn (nhưng tất nhiên cũng sẽ khó hiểu hơn) như sau:

Trong đó A là array cần sort, p là index đầu tiên của A: p = 1, r là index cuối cùng của A

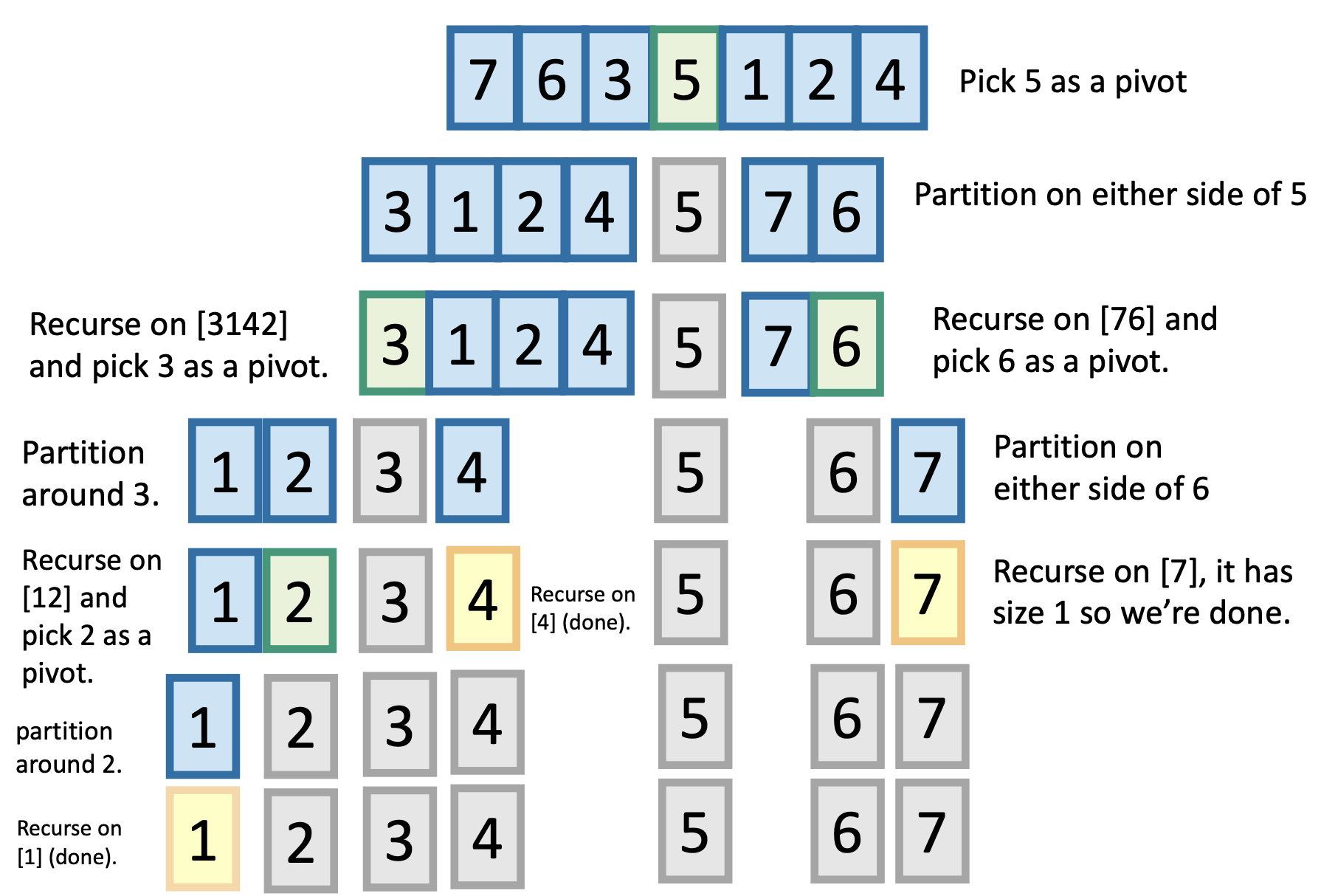
Theo cách implement này thì pivot luôn được chọn là phần tử cuối cùng (x = A[r] trong hàm PARTITION) nên cũng có thể coi là ngẫu nhiên về mặt độ lớn. Sau đó hàm PARTITION này sẽ return về q là thứ tự của pivot x trong array (pivot x bé thứ q trong array A). Trong VD minh hoạ bên dưới thì pivot x=4 (phần tử cuối cùng), trả về q=4 (giá trị x này bé thứ 4 trong array)

Để dễ hình dung thì Algorithm này sử dụng 2 index i và j, index j để scan lần lượt từng giá trị array, còn index i để maintains sao cho các phần tử từ p cho tới i thì luôn < pivot, còn các phần tử từ i+1 tới j thì luôn >= pivot. Bước cuối cùng pivot A[r] được đổi chỗ về đúng thứ tự của nó trong array

2. Randomization

Vì việc chọn pivot là randomly nên ta chỉ có thể tính được expected (kì vọng) runtime của giải thuật.

Trước hết ta nhận thấy mọi cặp phần tử trong array chỉ có thể được so sánh với nhau tối đa1 lần (1 lần hoặc 0 lần). Chẳng hạn trong hình dưới, khi số 5 được chọn làm pivot, nó sẽ được so sánh với tất cả các số khác đúng 1 lần, còn cặp số 3 và số 6 chẳng hạn, thì sẽ không bao giờ được so sánh với nhau.

Như vậy, nếu gọi Xi,j là biến đại diện cho việc phần tử bé thứ i và phần tử bé thứ j có được so sánh với nhau hay không thì Xi,j = {0, 1}

Tổng số lần so sánh được thực hiện trong Quick Sort là:

Kì vọng của tổng số lần so sánh được thực hiện:

Gọi a, b là giá trị của phần tử bé thứ i và phần tử bé thứ j, ta hình dung việc chọn pivot có thể xảy ra các trường hợp như sau:

• TH1: Nếu chọn pivot rơi vào a hoặc b thì Xij = 1
• TH2: Nếu chọn pivot rơi vào a < pivot < b thì Xij = 0
• TH3: Nếu chọn pivot rơi vào pivot < a hoặc pivot > b thì Xij = unknown, lúc này a và b sẽ rơi vào cùng 1 partition, và phải chọn lần pivot tiếp theo thì mới quyết định được giá trị của Xij

Như vậy tại mỗi lần quyết định được giá trị của Xij, P(Xij = 1) = số lần TH1 xảy ra/ (số lần TH1 + số lần TH2 xảy ra) = 2/j-i+1

Vậy:

Xét số H = 1 + 1/2 + 1/3 + 1/4 +… gọi là ‘harmonic number’ và nó có giá trị trong khoảng: ln(n) < Hn < 1 + ln(n). Chứng minh như sau:

• Đường blue nhận giá trị 1/k trong khoảng [k, k+1)
• Đường red nhận giá trị 1/x trong khoảng [1, ∞)
• Đường green nhận giá trị 1/k+1 trong khoảng [k, k+1)

Gọi phần diện tích dưới đường curve (area under the curve – AUC) tạo bởi đường blue, red, green lần lượt là AUC_blue, AUC_red và AUC_green. Ta có: AUC_green < AUC_red < AUC_blue, hay:

(1)

(2)

Từ (1) và (2) dễ dàng suy ra: ln(n) < Hn < 1 + ln(n)

Quay trở lại với E[X] ta có:

Do đó expected runtime của Quick Sort là O(nlogn)

Tất nhiên trong trường hợp Worst Case (mặc dù rất khó xảy ra) thì độ phức tạp của Quick Sort vẫn là O(n^2). Giả sử ta chọn phần tử bé thứ k làm pivot, khi đó độ phức tạp của giải thuật sẽ là: T(n) = T(k-1) + T(n-k) + O(n) vì lúc này original array với size n bị chia thành 2 subarray: L gồm (k-1) phần tử < phần tử bé thứ k, và R gồm (n-k) phần tử > phần tử bé thứ k, và O(n) time cho thao tác PARTITION.

Nếu chẳng may lúc nào pivot cũng là phần tử MAX (tức k=n), hoặc phần tử MIN (tức k=1) thì trong cả 2 trường hợp này, độ phức tạp của giải thuật sẽ là:

T(n) = T(n-1) + O(n)

= T(n-2) + 2O(n)

= T(n-3) + 3O(n)

= …

= T(n-i) + iO(n)

Tại điều kiện dừng i = n: T(n) = T(0) + nO(n) ~ O(n^2)

Tuy nhiên do trường hợp Worst Case rất khó xảy ra, cộng thêm với việc implement rất hiệu quả (không phải tạo ra nhiều bản copy của array như Merge Sort, mà có thể thực hiện in-place được) nên Quick Sort vẫn được dùng nhiều trong thực tế (Java, C, Unix, g++)