1. Comparison-based

Ta đã được xem một vài giải thuật sorting như: Insertion Sort, Merge Sort, Quick Sort. Các giải thuật này thuộc nhóm comparison-based, tức là dựa trên các phép so sánh giữa các phần tử. Độ phức tạp tốt nhất của nhóm giải pháp này hiện tại đang là O(nlog(n)), liệu có thể tốt hơn không? O(n) thôi chẳng hạn?

Câu trả lời là Có, tuy nhiên không thể dựa trên các phép so sánh, bởi độ phức tạp tối thiểu của nhóm comparison-based là Ω(n*log(n)).

Thực vậy, việc sort các phần tử dựa trên phép so sánh giống như đi tìm path của 1 decision tree mà lá của decision tree này là tất cả các khả năng sort có thể xảy ra.

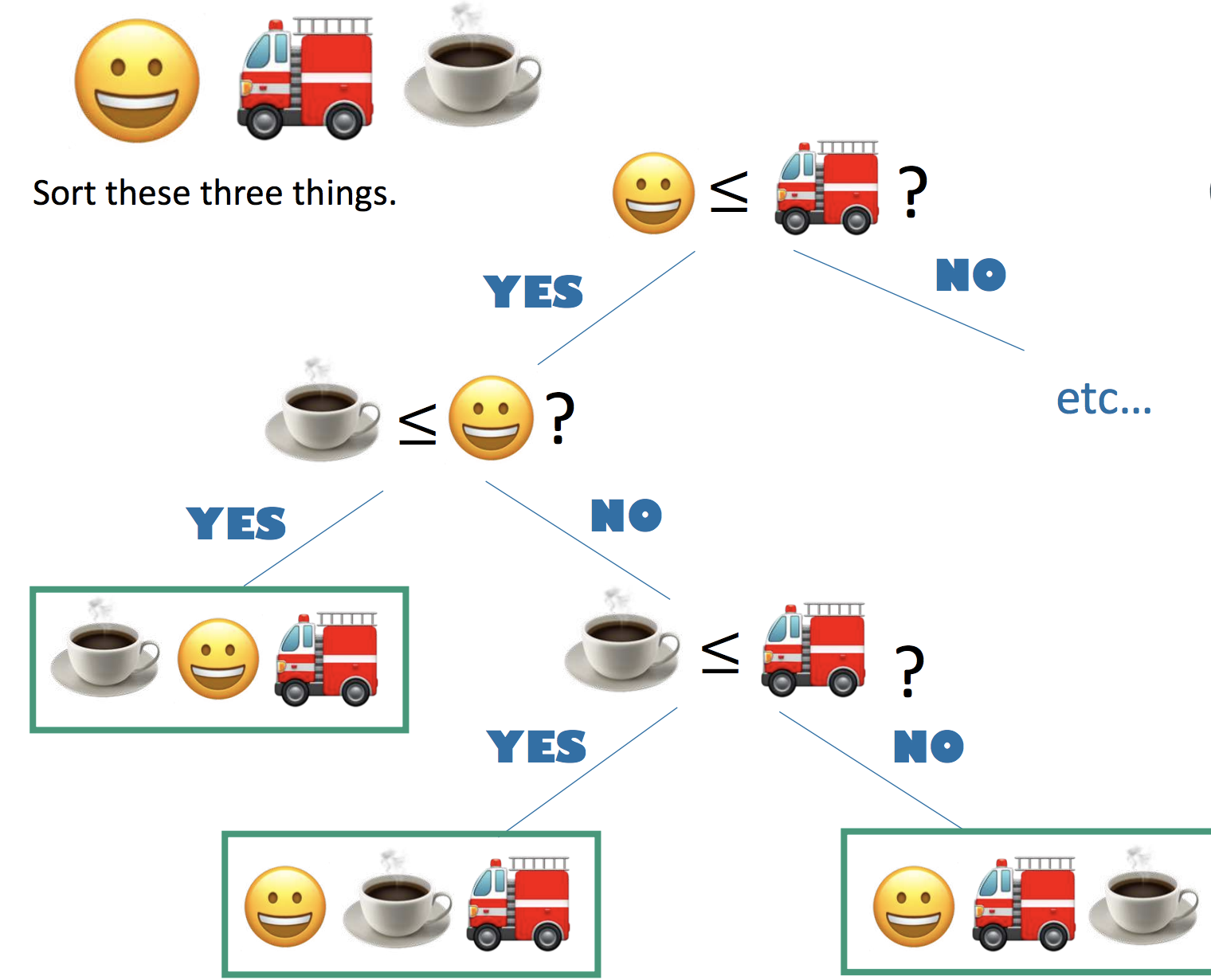
Trường hợp tồi nhất – tức phải thực hiện nhiều phép so sánh nhất <–> longest path của decision tree, và ta sẽ chứng minh longest path này >= n*log(n) với n là số phần tử cần phải sort 

• Có n! cách sắp xếp n phần tử –> decision tree phải có ít nhất n! lá (1)
• Gọi h là độ cao của decision tree thì số lá tối đa mà nó có được là: 2^h lá (2)

Từ (1) và (2) ta có: 2^h >= n! <–> h >= log(n!)

Do n! ~ (n/e)^n (Stirling’s approx) –> log(n!) ~ n*log(n/e)

Vậy h >= n*log(n)

Do đó mọi giải thuật sort dựa trên phép so sánh luôn có độ phức tạp tối thiểu là: Ω(n*log(n))

Vậy làm thế nào để sort với độ phức tạp chỉ O(n)? Ta cần 1 giải pháp khác mà không dựa vào comparison-based. Trước hết, hãy bắt đầu với một version đơn giản: Bucket Sort

2. Bucket Sort

Ý tưởng của Bucket Sort như sau:

1. Tạo một array A gồm r bucket, mỗi bucket là 1 linked list
2. Với mỗi phần tử có key=k trong array, nối nó vào cuối của linked list A[k]
3. Cuối cùng lần lượt nối tất cả các linked list: A[0], A[1],…,A[r-1]

Analysis

Tại bước 2, ta cần iterate lần lượt tất cả phần tử của array để đưa nó vào bucket tương ứng

Tại bước 3, ta cần iterate lần lượt r buckets để build thành array đã được sorted

Tổng cộng ta có O(n+r) runtime hay tổng quát hoá là O(n) 

Problem?

Điều gì xảy ra nếu các phần tử trong array có giá trị vô cùng lớn? Ta sẽ phải tạo ra cực kì nhiều buckets như thế này chăng? Hãy cùng xem cách giải quyết của Radix Sort

3. Radix Sort

Ý tưởng của Radix Sort là thực hiện Bucket Sort lần lượt từ chữ số ngoài cùng, từ bên phải qua bên trái

Analysis

Với mỗi một chữ số (từ 1 to L) ta cần O(n) run time để thực hiện Bucket Sort. Vậy tổng cộng Radix Sort cần L*O(n), hay tổng quát hoá là O(n) runtime

Problem?

Ta thấy Radix Sort rất hiệu quả khi ta cần sort những số nguyên nhỏ. Tuy nhiên nó cũng sẽ có những hạn chế sau khi so với những giải pháp comparison-based:

• Thời gian tính nếu chẳng may có một phần tử trong array có giá trị vô cùng lớn? (tức rất nhiều số chữ số)
• Cần nhiều memory để lưu bucket, trong khi Quick Sort có thể thực hiện in-place
• Gặp vấn đề khi các phần tử không còn là số nguyên? (3,14…), các phần tử là số thập phân? (2/3), các phần tử là số âm? (-123..) trong khi những giải pháp comparison-based có thể dễ dàng so sánh các phần tử kiểu này một cách nhanh chóng