Cùng một bài toán có thể sẽ có nhiều cách giải quyết, vậy làm thế nào để ta có thể đánh giá cách giải nào tốt hơn. Chẳng hạn để sắp xếp 1 list các number, hãy so sánh độ phức tạp của 2 phương pháp: Merge Sort & Insertion Sort

1. Insertion Sort

Insertion Sort là một phương pháp sắp xếp rất thuận theo ‘tự nhiên’. Ý tưởng như sau:

1. Duyệt lần lượt từng phần từ từ phần tử thứ 2 trở đi
2. Với mỗi lần duyệt như vậy, so sánh phần tử đang được duyệt hiện tại với các phần tử trước nó, và di chuyển cho tới khi nó trở về đúng thứ tự sort

Pseudocode:

Analysis:

Có bao nhiêu bước so sánh trong Insertion Sort? Trong vòng loop for ta có n iterates với n ~ độ dài của list. Với mỗi iteration, ta thực hiện m phép so sánh giữa A[i] và m phần tử trước nó (m<n). Tổng cộng ta có m*n phép so sánh. Khi n tiến tới vô cùng, m cũng sẽ tiến tới vô cùng, thì để đơn giản ta nói rằng độ phức tạp của giải thuật là O(n*n) hay O(n^2)

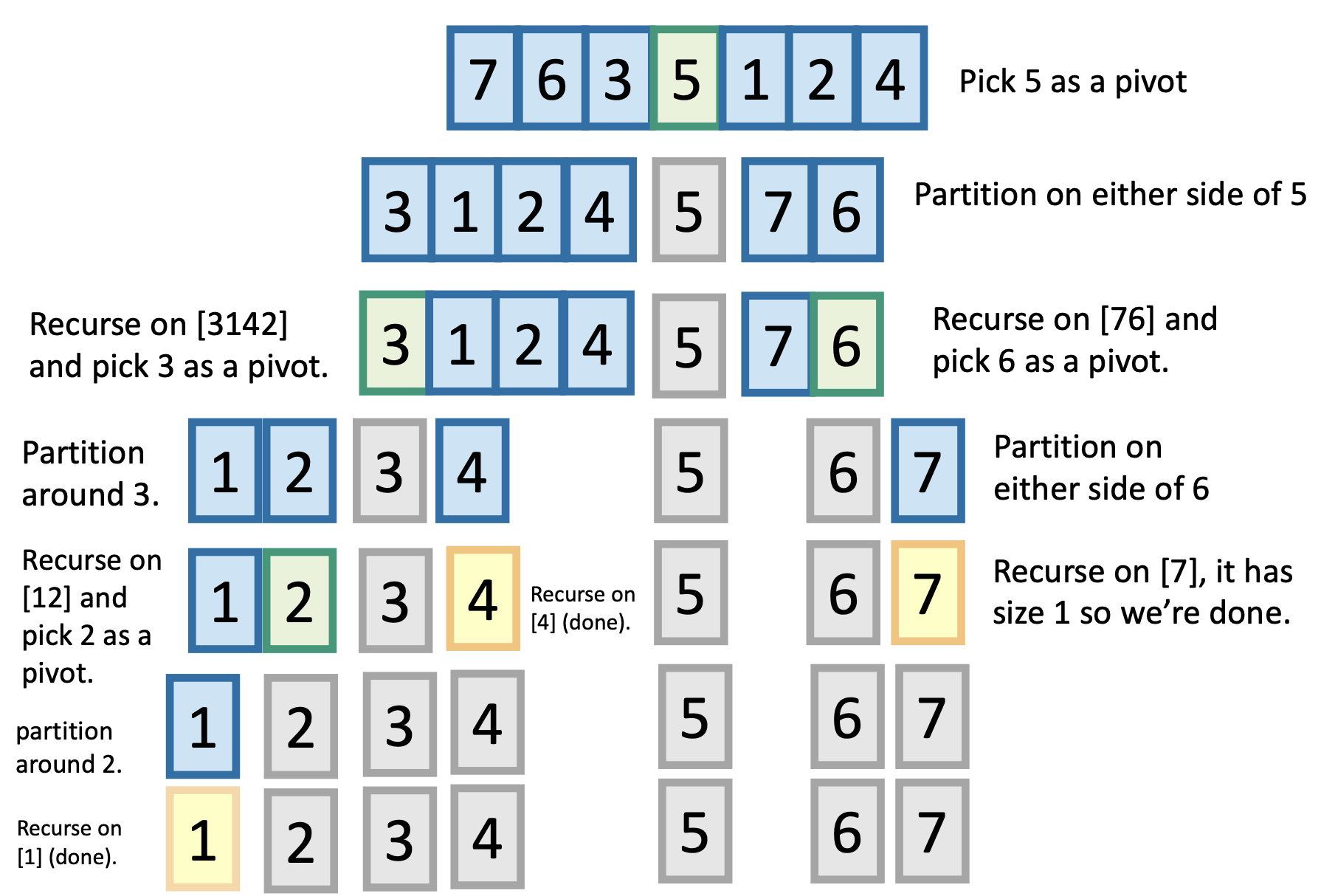
2. Merge Sort

Merge Sort sử dụng chiến lược Divide-And-Conquer, một trong những chiến lược quan trọng trong thiết kế giải thuật. Chúng ta sẽ còn gặp pattern này rất nhiều trong các bài về sau. Tuy nhiên về cơ bản thì nó chia original problems thành các subproblems nhỏ hơn, giải quyết các subproblems rồi combine kết quả lại. Chẳng hạn ý tưởng của giải thuật Merge Sort như sau:

1. Chia original array thành 2 sub array (‘Left’ array & ‘Right’ array)
2. Sort ‘Left’ array & ‘Right’ array
3. Merge 2 sorted array trên

Bước 1 đơn giản chỉ cần chia đôi original array ra thành 2 nửa (Left và Right)

Bước 2: Làm thế nào để Sort ‘Left’ array & ‘Right’ array? Với mỗi array đó, chúng ta lại chia nhỏ thành 2 sub array (Left và Right), sort chúng, sau đó combine lại. Quá trình đó cứ diễn ra như vậy (gọi là Recursive) cho đến khi không chia 2 được nữa (gặp điều kiện dừng): đó là khi độ dài của sub array <= 1. Khi này thì ta khỏi phải sort nữa vì array chỉ còn 1 phần tử (Algorithm 2)

Bước 3: Làm thế nào để Merge 2 sub array đã được sorted? VD: array Left = [3,4,6,8] và array Right = [1,2,5,7]? Cơ bản là với mỗi array ta cho 1 cái index i và j chạy từ phần tử đầu tiên và so sánh A[i] với B[j] coi chú nào bé hơn thì add vào cái array bự đang trống, đồng thời index của bên sub array có giá trị bé hơn được tăng lên 1 (Algorithm 3)

Pseudocode:

Analysis:

Có bao nhiêu bước diễn ra ở phần Merge Sort? Giả sử đó là T(n) với n là độ dài của original array. Theo algorithm 2, ta thấy: T(n) = 2*T(n/2) + các bước ở phần Merge(L, R)

Có bao nhiêu bước diễn ra ở phần Merge(L,R) với L, R là 2 sorted array có độ dài n/2? –> Có n bước (theo Algorithm 3)

Do đó: T(n) = 2T(n/2) + n

= 2(2T(n/4)+n/2)+n = 4T(n/4) + 2n

= 4(2T(n/8)+n/4) + 2n = 8T(n/8)+3n

= ..

= 2^i*T(n/2^i)+i*n

Khi tới điều kiện dừng: i = log(n) ta có T(n) <= n*T(1)+n*log(n) = n+nlog(n) = n(1+log(n)). Và khi n tiến tới vô cùng, nó sẽ ~ nlog(n). Để đơn giản, ta nói độ phức tạp của giải thuật là O(nlog(n))

3. Độ phức tạp của giải thuật (complexity)

Giả sử f(n) là độ phức tạp của giải thuật với input size là n

• Big O: Ta nói f(n) = O(g(n)) nếu f(n) <= c*g(n) khi n tiến ra vô cùng, hay O(g(n)) là chặn trên của f(n)
• Big Omega: Ta nói f(n) = Omega(g(n)) nếu f(n) >= c*g(n) khi n tiến ra vô cùng, hay Omega(g(n)) là chặn dưới của f(n)
• Big Theta: Ta nói f(n) = Theta(g(n)) nếu c1*g(n) <= f(n) <= c2*g(n), hay O(g(n)) là chặn trên của f(n) và Omega(g(n)) là chặn dưới của f(n)

Thường thì người ta chỉ quan tâm tới Big O, và khi nói tới độ phức tạp của giải thuật là người ta mặc định là Big O, tức chặn trên của f(n). VD: Insertion Sort có độ phức tạp là O(n^2) vì f(n) <= g(n) = n^2, Merge Sort có độ phức tạp là O(n*log(n)) vì f(n) <= g(n) = n*log(n).

Từ đây ta thấy nếu n tiến ra vô cùng, độ phức tạp của Merge Sort sẽ nhỏ hơn nhiều độ phức tạp của Insertion Sort (vì n*log(n) < n*n) dẫn tới việc Merge Sort chạy nhanh hơn nhiều so với Insertion Sort.

4. The Master Method

Với những bài toán có liên quan tới recurrences, khi mà sub-problems có cùng size (giống như Merge Sort), ta có thể sử dụng một phương pháp gọi là Master Method để tính độ phức tạp của giải thuật. Đó là khi T(n) có dạng tổng quát: T(n) = a*T(n/b) + O(n^d) trong đó: a >= 1, b >= 1, thì độ phức tạp T(n) là:

VD trong Merge Sort ta có a=2, b=2, d=1, do đó T(n) = O(nlog(n))