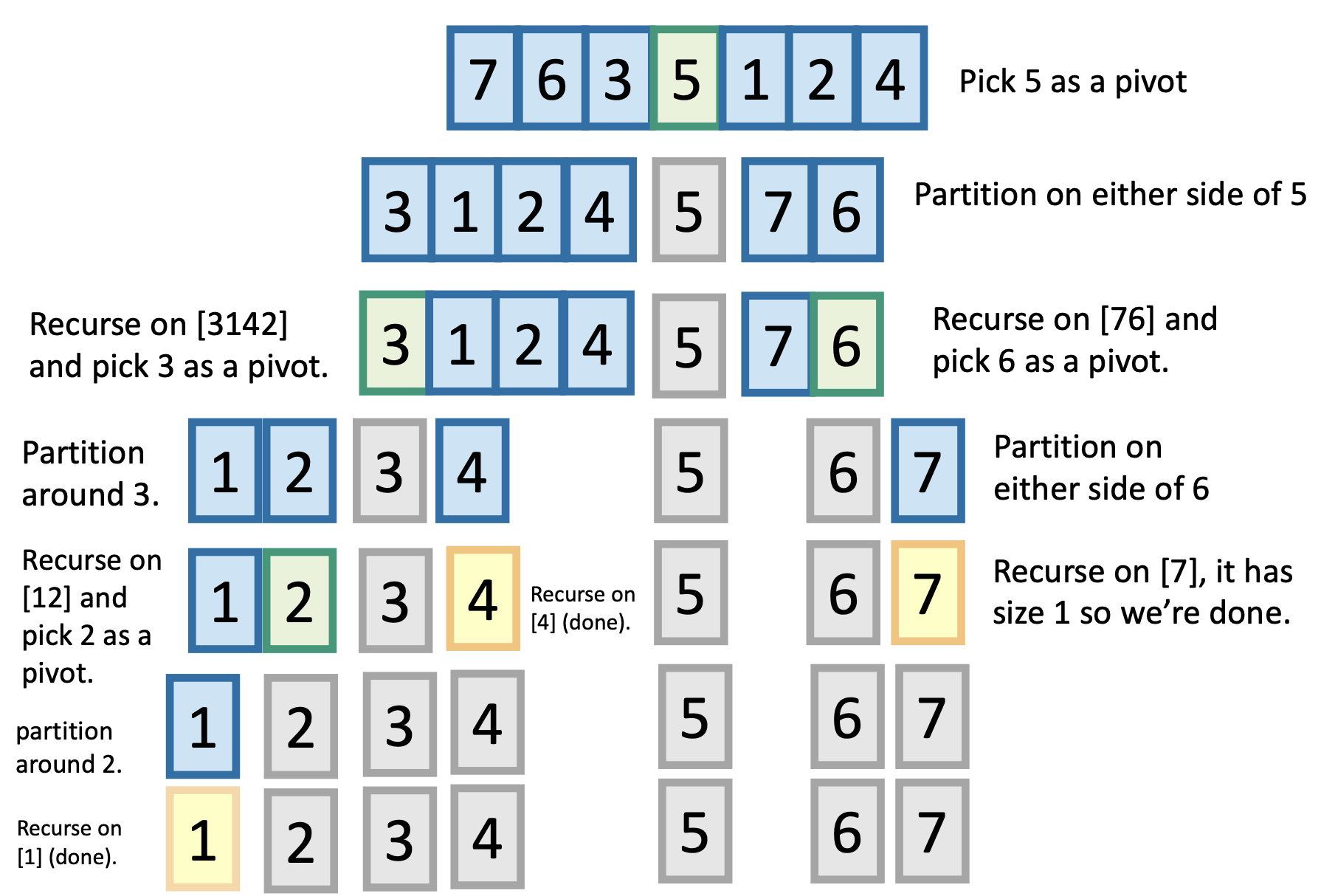
Trong các bài trước chúng ta đã được làm quen với mẫu thiết kế giải thuật kiểu Divide and Conquer, tức là chia nhỏ problem ban đầu thành các subproblems, giải quyết các subproblems đó bằng cách chia nhỏ chúng thành các subproblems tiếp theo và cứ recursive như vậy. 2 ví dụ điển hình của mẫu thiết kế này đó là Merge Sort và Quick Sort.

Tuy nhiên trong một số bài toán, khi các subproblems lặp lại nhau, việc recursive sẽ khiến cho tính toán bị lặp và không hiệu quả. Chẳng hạn tính số Fibonaci được định nghĩa như sau:

Cách giải sử dụng recursive:

Minh hoạ cho việc tính toán Fibonacci với n=5 như sau:

Ta thấy tại 1 giá trị (chẳng hạn n=2), việc tính toán bị lặp lại rất nhiều lần. Nếu n càng lớn thì số lần tính toán lặp lại càng nhiều, thời gian tính sẽ tăng theo hàm số mũ. Thực vậy, số lần phải tính của Fibonacci(n) giống như tổng số node của 1 binary tree có chiều cao n, và đó là: 2^n. Vậy độ phức tạp của giải thuật này là O(2^n)

Do các subproblems này có tính lặp lại nên ta có thể nghĩ tới giải pháp lưu kết quả của các subproblems, từ subproblems nhỏ nhất, sau đó build dần lên (bottom-up), để tránh việc phải tính lại. Đó cũng chính là tư tưởng của Dynamic Programming.

Chẳng hạn với bài toán Fibonacci ở trên, ta tính lần lượt bottom up như sau:

• F(2) = F(1) + F(0)
• F(3) = F(2) + F(1)
• …

Dễ thấy thời gian tính lúc này chỉ còn là O(n), tốt hơn rất nhiều so với giải pháp Recursive ban đầu. Dynamic programming là một giải thuật cực kì hiệu quả để giải quyết các bài toán mà chúng có thể tách nhỏ thành các subproblems và các subproblems này có tính lặp lại. Phần tiếp theo ta hãy cũng xem xét 1 số bài toán được giải quyết bằng Dynamic Programming.

1. Longest Common Subsequence

Ta nói Z là subsequence của X nếu như có thể tạo ra Z bằng cách xoá kí tự từ X. Ví dụ: baab là subsequence của abracadabra. Bài toán đặt ra là: cho 2 sequence X và Y, tìm Z là subsequence chung dài nhất – longest common subsequence (LCS) của X và Y. Ví dụ, X = abracadabra và Y = bxqrabry thì Z = LCS(X, Y) = brabr

Đây là bài toán có khá nhiều ứng dụng trong thực tế:

• Trong sinh học: những loài giống nhau thì có common subsequence dài
• Phép so sánh diff trong unix command
• Phép merging trong version control: svn, git, etc…

Gọi LCS(X, Y) là subsequence chung dài nhất của X và Y thì LCS(X, Y) có thể rơi vào 1 trong 2 cases:

• Nếu X[-1] = Y[-1] thì LCS(X, Y) = LCS(X[:-1], Y[:-1]) + 1
• Nếu X[-1] != Y[-1] thì LCS[X, Y] = max(LCS[X, Y[:-1], LCS(X[:-1], Y])

và bài toán có thể giải quyết bằng Recursive với base case: LCS(X, Y) = 0 nếu len(X) = 0 hoặc len(Y) = 0

Có thể thấy giải pháp Recursive ở trên sẽ gọi đi gọi lại nhiều lần hàm tính LCS(x, y) và bị lặp giống như bài toán Fibonacci. Bài toán này có thể được giải quyết bằng Dynamic Programming như sau:

Gọi C[i, j] là subsequence chung dài nhất của X[:i] và Y[:j] thì C[i, j] có thể rơi vào 1 trong 2 cases:

• Nếu X[i] = Y[j] thì C[i, j] = C[i-1, j-1] + 1
• Nếu X[i] = Y[j] thì C[i, j] = max(C[i, j-1], C[i-1, j])
• Base case: C[0, j] = C[i, 0] = 0

Độ phức tạp của giải pháp Dynamic Programming trên là O(nm).

2. Knapsack Problem

Đây là một bài toán kinh điển trong tối ưu tổ hợp, nội dung như sau: có n items, mỗi item có value và weight tương ứng. Có một cái túi (knapsack) với sức chứa tối đa là W. Hãy chọn items chất vào túi sao cho maximize được value? Ví dụ: túi có sức chứa W=10 và 4 items như bảng dưới:

Bài toán này có 2 versions:

• Unbounded Knapsack: Mỗi item có thể chọn bao nhiêu lần cũng được. Ở ví dụ trên, ta chọn 2 item B + 2 item D. Tổng weight = 10, và tổng value = 42
• 0-1 Knapsack: Mỗi item chỉ được chọn tối đa 1 lần. Ở ví dụ trên, ta chọn item A + item C. Tổng weight = 10 và tổng value = 40

2.1 Unbounded Knapsack Problem

Gọi K(x) optimal value mà knapsack có thể lấy với capacity x. Khi đó:

2.2 0-1 Knapsack Problem

Ở version này, ngoài việc phải sử dụng 1 biến x để keep track size của knapsack như trên, ta sẽ phải dùng thêm 1 biến j nữa để keep track items nào được sử dụng (vì mỗi item chỉ được chọn tối đa 1 lần)

Gọi K(x, j) là maximum value mà knapsack có được với capacity x, và chỉ dùng những items từ thứ 1 tới thứ j trong tổng số n items. Khi đó tại K(x, j) có thể có 2 cases:

• Không dùng item j: Khi này knapsack với capacity x đạt optimal value với j-1 items trước đó (1, 2, 3, …, j−1) –> K(x, j-1)
• Có dùng item j: Khi này knapsack với capacity x − w_j đạt optimal value với j-1 items trước đó (1, 2, 3, …, j−1) –> K(x-w_j, j-1)

Do đó: